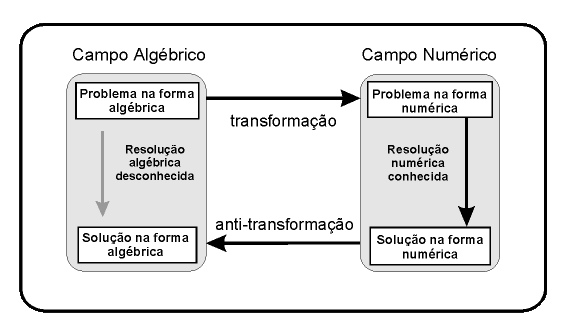
O que é a Transformada Numérica
O que é a Transformada Numérica
|
Todo o texto desta página, bem como das demais páginas sobre a TN, pressupõe que o leitor conheça Álgebra Booleana ou Cálculo Proposicional |
| O que é a TN | Definições | Aplicações da TN |
| Volta ao Índice Geral da TN | ||